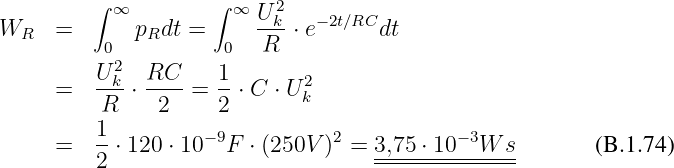Übungsaufgaben zum elektrischen Potentialfeld

Lösung zur
Aufgabe 10.7.1
(Kondensator)

Elektrische Feldstärke
$U0- -1000V---- 5 E0 = d0 = 2 ⋅ 10 −3m = 5-⋅ 10-V-∕m$
Elektrische Flussdichte
$D0 = ϵE0 = ϵ0ϵrE − 12 A-s- = 8,85 ⋅ 10 V m ⋅ 7 ⋅ 500.000V ∕m − 6 2 = 31,00-⋅ 10--As∕m-- (B.1.2)$
Vorhandene Ladung
$Q0 = Ψ = D0A = 31 ⋅ 10− 6As∕m2 ⋅ 0,1m2 = 3,1 ⋅ 10−6As (B.1.3) ------------$

Lösung zur
Aufgabe 10.7.2
(Kondensator)

Elektrische Flussdichten
$Q 1,5 ⋅ 10− 6As D1 = D2 = --0 = ------------- A 900 ⋅ 10 −4m2 = 16,7-⋅ 10−6As-∕m2 (B.1.4)$
Elektrische Feldstärken
$−6 2 E1 = -D1--= ----16,7 ⋅-10-As-∕m------- ϵ0ϵr1 8,85 ⋅ 10− 12 A s∕(V m ) ⋅ 2,5 = 7,53 ⋅ 105V ∕m (B.1.5) --------------$
und
$−6 2 E2 = -D2--= ----16,7 ⋅-10-As-∕m------- ϵ0ϵr2 8,85 ⋅ 10− 12 A s∕(V m ) ⋅ 4,5 = 4,18 ⋅ 105V ∕m (B.1.6) --------------$
Teilspannungen
$U = E d = 7,53 ⋅ 105V ∕m ⋅ 10 −3m 1 1 1 = 753V-- (B.1.7)$
und
$5 −3 U2 = E2d2 = 4,18 ⋅ 10 V∕m ⋅ 1,5 ⋅ 10 m = 627V-- (B.1.8)$
Kondensatorspannung
$U0 = U1 + U2 = 753V + 627V = 1380V--$ (B.1.9)

Lösung zur
Aufgabe 10.7.3
(Kondensator)

Gesuchte Spannung

U1 100V U2 = ---⋅ d1 =------- ⋅ 0,5mm = 160V-- d2 0,8mm

(B.1.10)

Lösung zur
Aufgabe 10.7.4
(Kondensator)

Gesuchte Spannung

U2 = ϵrU1 = 7 ⋅ 200V = 1400V--

(B.1.11)

Lösung zur
Aufgabe 10.7.5
(Kondensator)

Gesuchte Spannung
$U1 = E1d1 = 111V ∕mm ⋅ 1mm = 111V--$ (B.1.12)
Spannung am verbleibenden Luftraum
$U2 = U0 − U1 = 500V − 111V = 389V--$ (B.1.13)

Lösung zur
Aufgabe 10.7.6
(Kondensator)

Gesuchte Spannungen
$U1 = E1d1 = 20V ∕mm ⋅ 0,4mm = 8V- U2 = E2d2 = 100V ∕mm ⋅ 0,6mm = 60V-- (B.1.14)$
Spannung
$U1′= U0 − U2 = 100V − 60V = 40V--$ (B.1.15)

Lösung zur
Aufgabe 10.7.7
(Kondensator)

Feldstärke

U0 E2 = d1------------ ϵr + (d0 − d1) --------500V---------- = 1mm-+ (2mm − 1mm ) 7 = 437,5V∕mm = 437,5kV-∕m- (B.1.16)

Lösung zur
Aufgabe 10.7.8
(Punktladung)

Elektrische Feldstärke
$⃗E = ⃗E1 + E⃗2 + ⃗E3 ∘ = (81,025kV ∕m ⁄ 30 ) + (27,008kV ∕m ⁄ − 90∘) ∘ − (54,016kV ∕m ⁄ 150 ) = (117,726kV-∕m-⁄-−-6,57∘) (B.1.17) ------------------------$

Winkel

α = −-6,57∘

(B.1.18)

Lösung zur
Aufgabe 10.7.9
(Punktladung)

Gesuchte Kraft
$F⃗ = F⃗13 + F⃗23 −4 ∘ = (2,70 ⋅ 10 N ⁄-45 ) + (2,70 ⋅ 10−4N ⁄-90∘) −4 ∘ = (5,00-⋅ 10-N-⁄-67,5-) (B.1.19)$

Winkel

α = 67,5∘

(B.1.20)

Lösung zur
Aufgabe 10.7.10
(Punktladung)

Gesuchte Kraft
$F⃗ = ⃗F12 + ⃗F32 − 4 ∘ = (1,43 ⋅ 10 N ⁄ 17 ) − (1,33 ⋅ 10− 4N ⁄ 90∘) − 4 ∘ = (1,64-⋅ 10--N-⁄ −-33,7-)- (B.1.21)$

Winkel

α = − 33,7 ∘ − 90 ∘ = −-123,7∘

(B.1.22)

Lösung zur
Aufgabe 10.7.11
(Punktladung)

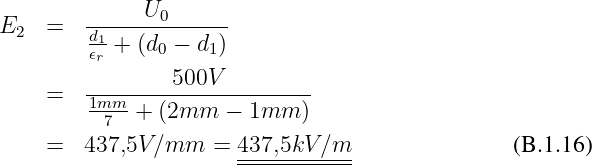
Erste gesuchte Ladung

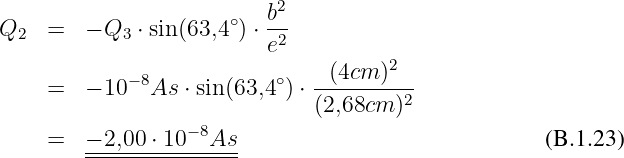
b2 Q2 = − Q3 ⋅ sin (63,4∘) ⋅-2 e −8 ∘ -(4cm-)2-- = − 10 As ⋅ sin(63,4 ) ⋅ (2,68cm )2 − 8 = − 2,00-⋅ 10-As- (B.1.23)

Zweite gesuchte Ladung

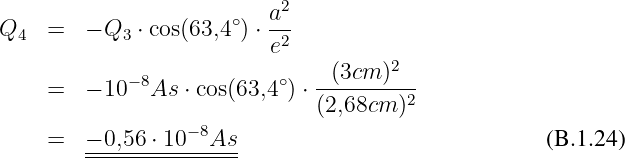
2 ∘ a-- Q4 = − Q3 ⋅ cos(63,4 ) ⋅e2 (3cm )2 = − 10 −8As ⋅ cos(63,4∘) ⋅------2- (2,68cm ) = − 0,56-⋅ 10−8As (B.1.24) ---------------

Lösung zur
Aufgabe 10.7.12
(Kugel)

Durchmesser der Kugel

d ≥ 2r = 2 ⋅ 6,7mm = 1,34cm-

(B.1.25)

Lösung zur
Aufgabe 10.7.13
(Kugel)

Kraft

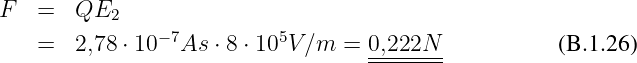
F = QE2 = 2,78 ⋅ 10− 7As ⋅ 8 ⋅ 105V∕m = 0,222N (B.1.26) --------

Lösung zur
Aufgabe 10.7.14
(Kondensator)

Gesuchte Gesamtkapazität

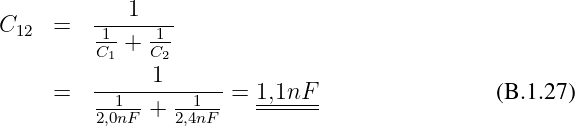
---1---- C12 = -1 + 1- C1 C2 ------1------ = --1--+ --1--= 1,1nF-- (B.1.27) 2,0nF 2,4nF

Lösung zur
Aufgabe 10.7.15
(Kondensator)

Gesuchte Dicke der Glimmerscheibe

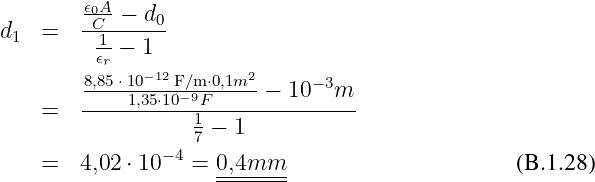
ϵ0A − d0 d1 = -C1----- ϵr − 1 8,85-⋅10−12F∕m⋅0,1m2 −3 = -----1,35⋅10−9F------−-10--m-- 17 − 1 −4 = 4,02 ⋅ 10 = 0,4mm-- (B.1.28)

Lösung zur
Aufgabe 10.7.16
(Kondensator)

Dicke der Glimmerplatte

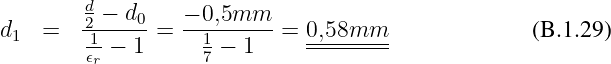
d− d − 0,5mm d1 = 21----0-= --1------ = 0,58mm-- (B.1.29) ϵr − 1 7 − 1 --------

Lösung zur
Aufgabe 10.7.17
(Kondensator)

Quotient der Kapazitäten

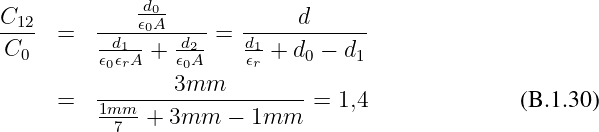
d C12- ----ϵ00A---- -----d------ C = --d1-+ d2- = d1 + d − d 0 ϵ0ϵrA ϵ0A ϵr 0 1 = --------3mm--------- = 1,4 (B.1.30) 1mm- + 3mm − 1mm 7

Lösung zur
Aufgabe 10.7.18
(Schaltung)

Spannung

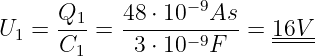Q1 48 ⋅ 10− 9As U1 = --- = ------−9----= 16V-- C1 3 ⋅ 10 F

(B.1.31)

die Spannung am Kondensator

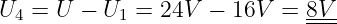U4 = U − U1 = 24V − 16V = 8V-

(B.1.32)

Spannung

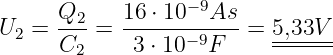− 9 Q2- 16-⋅ 10--As- U2 = C2 = 3 ⋅ 10− 9F = 5,33V--

(B.1.33)

Letzte gesuchte Spannung

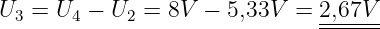U3 = U4 − U2 = 8V − 5,33V = 2,67V- ------

(B.1.34)

Lösung zur
Aufgabe 10.7.19
(Schaltung)

Gespeicherte Ladungen
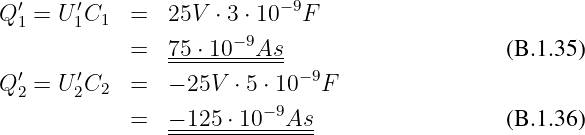
$Q ′= U′C = 25V ⋅ 3 ⋅ 10−9F 1 1 1 − 9 = 75-⋅ 10-As-- (B.1.35) Q ′= U′C2 = − 25V ⋅ 5 ⋅ 10 −9F 2 2 −9 = −-125-⋅ 10-As- (B.1.36)$
Widerstand zugeführte Energie
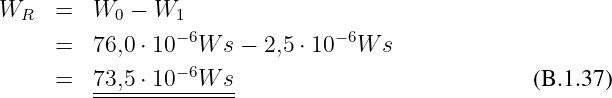
$WR = W0 − W1 = 76,0 ⋅ 10− 6W s − 2,5 ⋅ 10 −6W s − 6 = 73,5-⋅ 10-W--s (B.1.37)$

Lösung zur
Aufgabe 10.7.20
(Schaltung)

Spannung
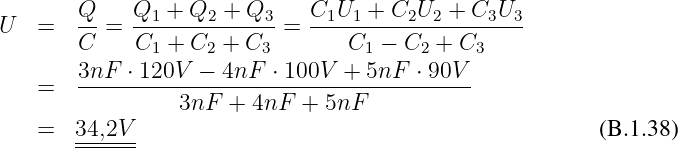
$Q Q1 + Q2 + Q3 C1U1 + C2U2 + C3U3 U = --= --------------= --------------------- C C1 + C2 + C3 C1 − C2 + C3 = 3nF-⋅-120V-−--4nF-⋅ 100V-+-5nF--⋅ 90V- 3nF + 4nF + 5nF = 34,2V- (B.1.38) ------$
In Wärme umgesetzte Energie
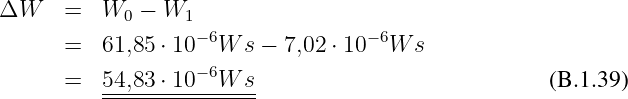
$ΔW = W0 − W1 −6 −6 = 61,85 ⋅ 10 W s − 7,02 ⋅ 10 W s = 54,83 ⋅-10−6W-s (B.1.39)$

Lösung zur
Aufgabe 10.7.21
(Schaltung)

Erste gesuchte Spannung

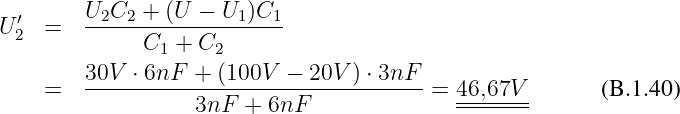
U C + (U − U )C U ′2 = --2-2----------1--1 C1 + C2 30V--⋅ 6nF-+-(100V-−--20V-) ⋅ 3nF = 3nF + 6nF = 46,67V- (B.1.40)

zweite

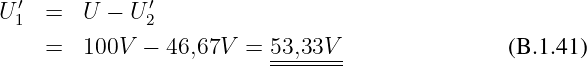
U ′ = U − U′ 1 2 = 100V − 46,67V = 53,33V- (B.1.41)

Lösung zur
Aufgabe 10.7.22
(Schaltung)

Gesuchte Spannung

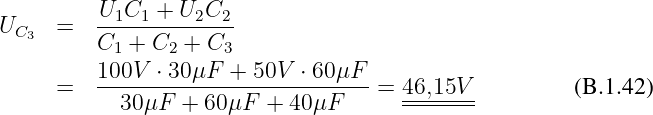
U1C1 + U2C2 UC3 = -------------- C1 + C2 + C3 = 100V--⋅ 30μF-+-50V-⋅-60μF- = 46,15V (B.1.42) 30μF + 60 μF + 40 μF -------

Lösung zur
Aufgabe 10.7.23
(Schaltung)

Erste gesuchte Spannung

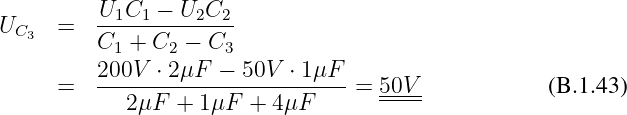
U = U1C1-−-U2C2--- C3 C1 + C2 − C3 200V ⋅ 2μF − 50V ⋅ 1μF = ------------------------= 50V-- (B.1.43) 2μF + 1μF + 4μF

Beide anderen Spannungen

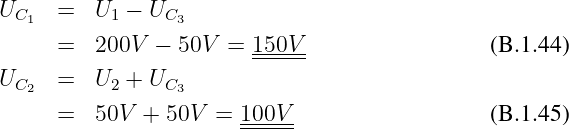
UC1 = U1 − UC3 = 200V − 50V = 150V-- (B.1.44) UC2 = U2 + UC3 = 50V + 50V = 100V-- (B.1.45)

Lösung zur
Aufgabe 10.7.24
(Schaltung)

Erste gesuchte Spannung

U = --U-C1---- 1 C1 + C234 36V ⋅ 10μF = -------------= 22,5V- (B.1.46) 10μF + 6μF

Zweite gesuchte Spannung

Q2 135 ⋅ 10 −6As U2 = --- = -------−-6---= 7,5V-- C2 18 ⋅ 10 F

(B.1.47)

Fehlenden Spannungen

U3 = U4 = U1 − U2 = 22,5V − 7,5V = 15V-- (B.1.48)

Lösung zur
Aufgabe 10.7.25
(Schaltung)

Ersten gesuchten Spannungen
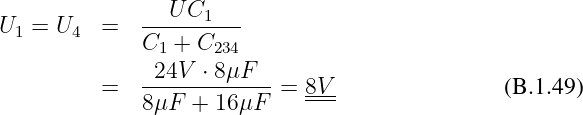
$U C1 U1 = U4 = ---------- C1 + C234 = -24V--⋅ 8μF--= 8V (B.1.49) 8μF + 16μF ---$
Weitere gesuchte Spannungen
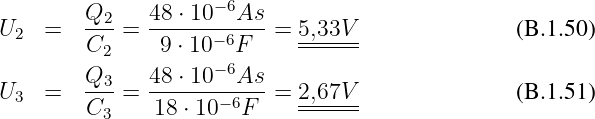
$Q 48 ⋅ 10 −6As U2 = --2 = ------------= 5,33V-- (B.1.50) C2 9 ⋅ 10 −6F ------ Q3 48 ⋅ 10 −6As U3 = C-- = -18-⋅ 10−6F-= 2,67V-- (B.1.51) 3$
In Wärme umgesetzte Energie
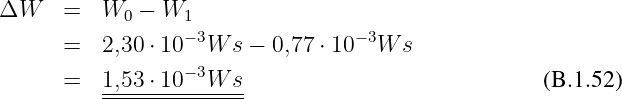
$ΔW = W0 − W1 = 2,30 ⋅ 10−3W s − 0,77 ⋅ 10− 3W s = 1,53-⋅ 10−3W-s (B.1.52)$

Lösung zur
Aufgabe 10.7.26
(Kugeln)

Kapazität
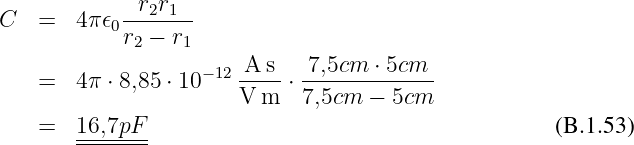
$r r C = 4πϵ0---2-1- r2 − r1 −12-A-s -7,5cm-⋅ 5cm- = 4π ⋅ 8,85 ⋅ 10 V m ⋅7,5cm − 5cm = 16,7pF (B.1.53) -------$
Maximal zulässige Spannung
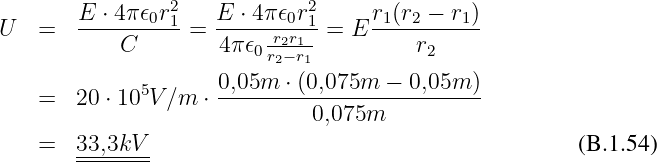
$E ⋅ 4π ϵ0r2 E ⋅ 4π ϵ0r2 r1(r2 − r1) U = --------1-= -----r2r11= E ----------- C 4π ϵ0r2− r1 r2 5 0,05m ⋅ (0,075m − 0,05m ) = 20 ⋅ 10 V∕m ⋅-------------------------- 0,075m = 33,3kV--- (B.1.54)$

Lösung zur
Aufgabe 10.7.27
(Kugeln)

Kapazität
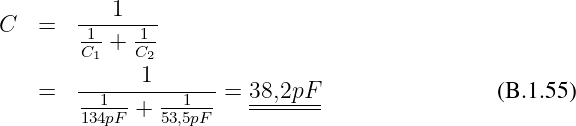
$1 C = -1----1- C1 + C2 1 = ---1--+---1---= 38,2pF- (B.1.55) 134pF 53,5pF$
Maximal zulässige Spannung
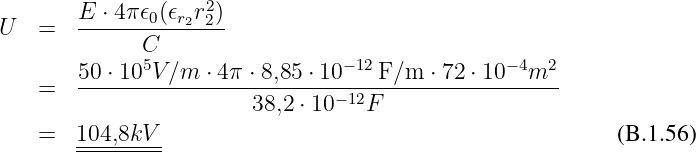
$2 U = E-⋅ 4-πϵ0(ϵr2r2) C 50 ⋅ 105V ∕m ⋅ 4π ⋅ 8,85 ⋅ 10− 12 F∕m ⋅ 72 ⋅ 10−4m2 = -----------------38,2 ⋅ 10-−12F--------------- = 104,8kV-- (B.1.56)$
Werte für eine Skizze:
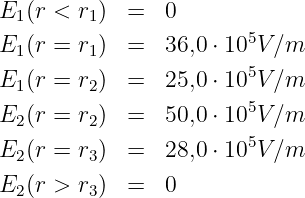
$E1(r < r1) = 0 E1(r = r1) = 36,0 ⋅ 105V ∕m 5 E1(r = r2) = 25,0 ⋅ 10 V ∕m E2(r = r2) = 50,0 ⋅ 105V ∕m E (r = r ) = 28,0 ⋅ 105V ∕m 2 3 E2(r > r3) = 0$

Lösung zur
Aufgabe 10.7.28
(Kugeln)

Gesuchte maximale Feldstärke

CU E = --------2-- 4πϵ0(ϵr2r2) ------62-⋅ 10-−12F-⋅ 50-⋅ 103V------ = 4π ⋅ 8,85 ⋅ 10 −12F∕m ⋅ 1225 ⋅ 10− 5m2 6 = 2,275 ⋅ 10 V ∕m = 22,75kV-∕cm- (B.1.57)

Lösung zur
Aufgabe 10.7.29
(Koax)

Kapazität
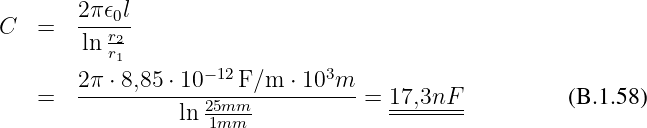
$2πϵ0l C = ---r2- ln r1 2π ⋅ 8,85 ⋅ 10 −12F∕m ⋅ 103m = ---------ln-25mm------------= 17,3nF-- (B.1.58) 1mm$
Gesuchte elektrische Feldstärke
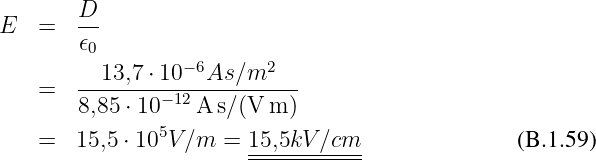
$E = D- ϵ0 13,7 ⋅ 10 −6As∕m2 = -------−-12---------- 8,85 ⋅ 10 A s∕(V m ) = 15,5 ⋅ 105V ∕m = 15,5kV ∕cm (B.1.59) -----------$

Lösung zur
Aufgabe 10.7.30
(Rohre)

Gesuchte Gesamtkapazität
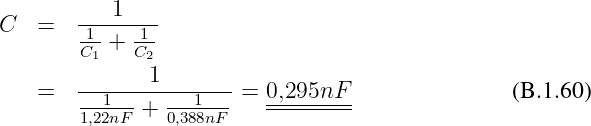
$1 C = -1----1- C1 + C2 1 = --1--------1--- = 0,295nF-- (B.1.60) 1,22nF + 0,388nF$
Gesuchte maximale Spannung
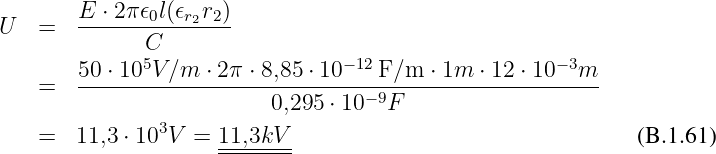
$E ⋅ 2πϵ0l(ϵr2r2) U = -------C------- 5 − 12 −3 = 50-⋅ 10-V-∕m-⋅ 2-π ⋅-8,85-⋅ 10-F∕m-⋅ 1m-⋅-12 ⋅ 10-m 0,295 ⋅ 10 −9F = 11,3 ⋅ 103V = 11,3kV (B.1.61) --------$

Lösung zur
Aufgabe 10.7.31
(Rohre)

Gesuchte maximale Feldstärke

E = ----CU------ 2πϵ0l(ϵr2r2) 0,295 ⋅ 10− 9F ⋅ 10 ⋅ 103V = ------------−12------------------------ 2π ⋅ 8,85 ⋅ 10 F ∕m ⋅ 1m ⋅ 24 ⋅ 10−3mm = 2,23 ⋅ 106V ∕m = 22,3kV ∕cm (B.1.62) -----------

Lösung zur
Aufgabe 10.7.32
(Kondensator)

Gesuchte gespeicherte Energie
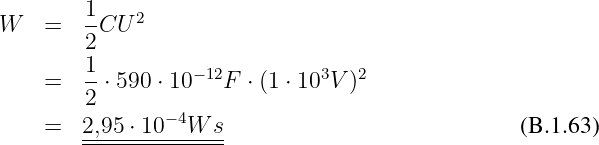
$1 W = -CU 2 2 = 1-⋅ 590 ⋅ 10−12F ⋅ (1 ⋅ 103V )2 2 = 2,95-⋅ 10-−4W-s (B.1.63) --------------$
Kraft
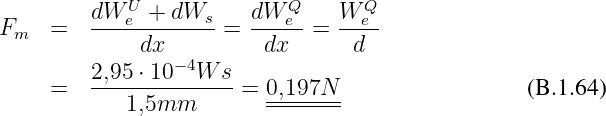
$U Q Q Fm = dW-e-+--dWs- = dW-e- = W-e- dx dx d 2,95 ⋅ 10-−4W-s = 1,5mm = 0,197N--- (B.1.64)$

Lösung zur
Aufgabe 10.7.33
(Kondensator)

Ladung
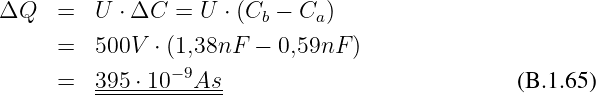
$ΔQ = U ⋅ ΔC = U ⋅ (Cb − Ca) = 500V ⋅ (1,38nF − 0,59nF ) − 9 = 395-⋅ 10--As- (B.1.65)$
Energie
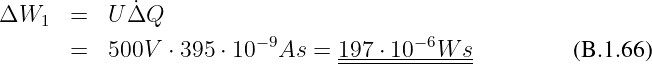
$˙ ΔW1 = U ΔQ = 500V ⋅ 395 ⋅ 10−9As = 197-⋅ 10−-6W-s (B.1.66)$
Gespeicherte Energie
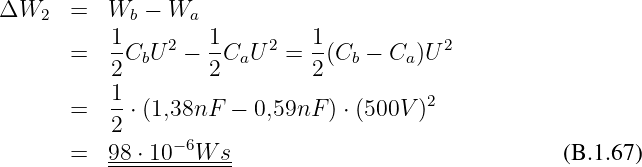
$ΔW2 = Wb − Wa = 1-C U 2 − 1C U2 = 1(C − C )U 2 2 b 2 a 2 b a 1- 2 = 2 ⋅ (1,38nF − 0,59nF ) ⋅ (500V ) −6 = 98-⋅ 10-W--s (B.1.67)$

Lösung zur
Aufgabe 10.7.34
(Kondensator)

Ladungsänderung
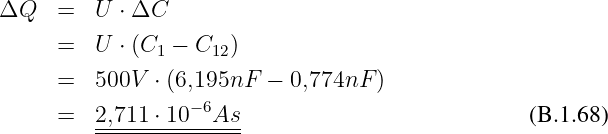
$ΔQ = U ⋅ ΔC = U ⋅ (C1 − C12) = 500V ⋅ (6,195nF − 0,774nF ) = 2,711-⋅ 10−6As (B.1.68) --------------$
Energieänderung der Spannungsquelle
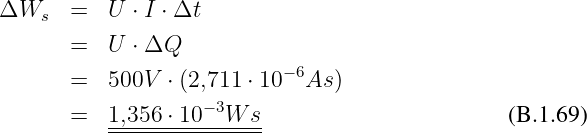
$ΔWs = U ⋅ I ⋅ Δt = U ⋅ ΔQ = 500V ⋅ (2,711 ⋅ 10−6As ) = 1,356 ⋅ 10− 3W s (B.1.69) ---------------$
Energieänderung des Kondensators
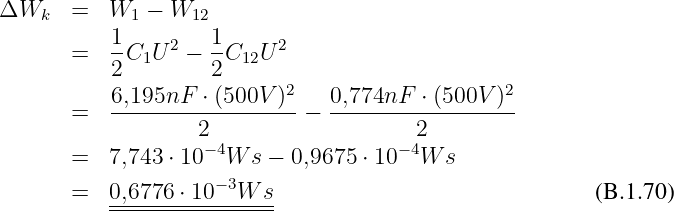
$ΔWk = W1 − W12 1- 2 1- 2 = 2 C1U − 2C12U 2 2 = 6,195nF--⋅ (500V-) − 0,774nF--⋅ (500V-) 2 2 = 7,743 ⋅ 10−4W s − 0,9675 ⋅ 10 −4W s = 0,6776 ⋅ 10−3W s (B.1.70) ----------------$
Energiebilanz
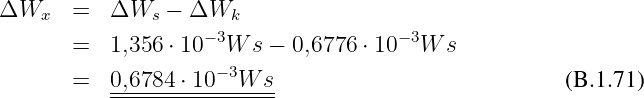
$ΔW = ΔW − ΔW x s −3 k −3 = 1,356 ⋅ 10 W s − 0,6776 ⋅ 10 W s = 0,6784 ⋅ 10−3W s (B.1.71) ----------------$
Diese Energie wird von außen durch die mechanische Vergrößerung des Plattenabstandes eingebracht.

Lösung zur
Aufgabe 10.7.35
(Kondensator)

Energie
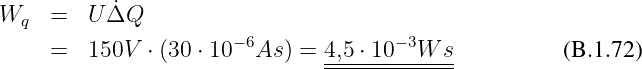
$Wq = U ˙ΔQ = 150V ⋅ (30 ⋅ 10−6As ) = 4,5 ⋅ 10− 3W s (B.1.72) -------------$
Energie
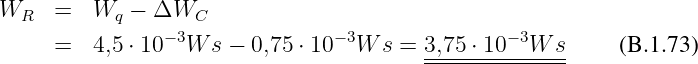
$W = W − ΔW R q −3 C − 3 −3 = 4,5 ⋅ 10 W s − 0,75 ⋅ 10 W s = 3,75 ⋅-10-W-s- (B.1.73)$

Beweis

∫ ∞ ∫ ∞ U 2 WR = pRdt = --k ⋅ e−2t∕RC dt 0 0 R Uk2 RC-- 1- 2 = R ⋅ 2 = 2 ⋅ C ⋅ U k 1 = --⋅ 120 ⋅ 10−9F ⋅ (250V )2 = 3,75-⋅ 10−-3W-s (B.1.74) 2

Da der Widerstandswert in der Endgleichung nicht mehr vorkommt ist die im Widerstand in Wärme umgesetzte Energie unabhängig vom tatsächlichen Widerstandswert!

B.1 Übungsaufgaben zum elektrischen Potentialfeld